[AGAL个人笔记]第四篇：加入深度(译，Z轴也叫深度坐标)

原文：Stage3D / AGAL from scratch. Part IV – Adding some depth

eg.如果你E文不错的话  还是看E文比较带劲。本人E文非常烂，若有偏差请指出。

关于Z轴的解释（角度理解）：

Stage3D，我认为这是3D的技术，但是为什么我们在上一节并没有用到Z轴坐标呢？如果你在上一节我分析代码的时候也跟着下载源码来编译，并且尝试修改其中的坐标看效果的话，你就会发现  没用（X,Y,Z,r,g,b）顶点中的Z数值，Z轴有何作用呢，下面我将解释。

——3D场景在2D中渲染，渲染出的区域叫做Clipspace（这个应该翻译为锥体裁剪之后的空间，还是投影变换后的空间？），CLIPSPACE（剪切空间）是屏幕的基础，屏幕上的每一个点 都会被映射到CLIPSPACE（剪切空间），然后才能被显示出来。（这个CLIPSPACE（剪切空间）就是这么一个东西   不理解没关系 如果要深入理解麻烦去找本计算机图形学）。

——之前说的屏幕坐标（X,Y,Z）每一个数值都是在闭区间[-1,1]其实表述并不完全正确，更准确的解释是，X,Y,Z 只有在闭区间[-1,1]的时候  才能映射在CLIPSPACE（剪切空间）上（也就是说 你所能看到的程序窗口大小 即为CLIPSPACE有效大小，所以我在之前也加了解释，坐标的有效数值是[-1,1]，坐标可以取任何值）。

——CLIPSPACE（剪切空间）的宽度（width）和高度（height）和程序的宽度高度一致，如果你写的是浏览器程序的话 那和浏览器的宽高一致，如果程序全屏 那就与显示器的宽度高度一致，一句话总结：CLIPSPACE的宽高与stage.stageWidth，stage.stageHeigh一致。CLIPSPACE（剪切空间）会随着程序显示舞台的改变而改变，而有效值一直都是[-1,1]，于像素值无关，相当于百分比，例如（0.5，0.5）在手机上是显示在中央，在浏览器上也是显示在中央，在独立的AIR程序上也是显示在中央，在IOS程序上也是如此。一句话概括CLIPSPACE（剪切空间）的特点：无论设备 还是舞台大小怎么变化 焦点始终集中在显示舞台上。现在CLIPSPACE的神秘面纱已经揭开，现在你应该能理解为什么设置顶点坐标为（2，1，0）的时候  舞台为什么显示不全了。

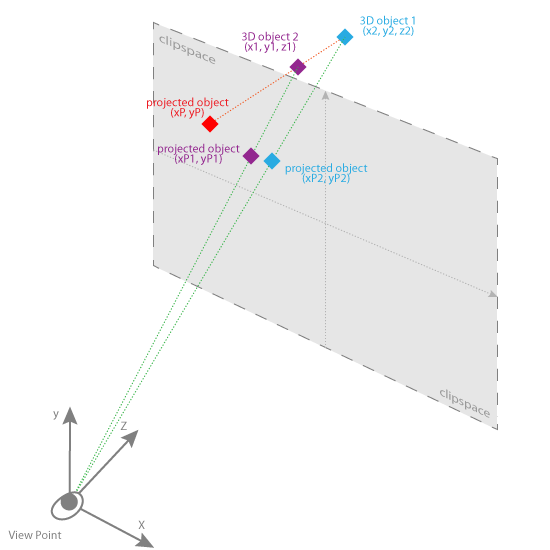
在上一篇中，我们仅仅输出每一个顶点的颜色到屏幕上，下图为Z轴不同的情况下的投射图：

在上图的三个点：

CLIPSPACE（剪切空间）上的点 ：

projected object（xP，yP）

3D虚拟点：

3D object2（x1，y1，z1）

3D object1（x2，y2，z2）

如果没用透视投影（不考虑Z）的话 那两个虚拟点 其实都和CILPSPACE（剪切空间）上的点重合（视觉上看），因为原点是视觉点，也就是说是你的眼睛，也就是说Stage3D模拟出来的3D世界中  立体坐标原点为你的眼睛。

透视投影：

透视投影是能在2D屏幕上渲染出3D效果的关键，透视是指一种远处的对象比离你较近的对象看起来似乎要小一些的概念。 透视也指如果你坐在一条笔直的道路中央，那么你实际看到道路边缘能够成为两条会聚的直线。这就是透视。 在3D项目中，透视至关重要。 如果没有透视技术，那么3D世界看起来就不真实。（暂时理解不了没关系 往下看），关于透视投影请移步传送门：Stage3D和透视投影的使用

以下是公式表示：

[cc lang=”java”]
xP = K1 * x / z
yP = K2 * y / z
[/cc]

（xP,yP）是2D屏幕上的物理点，（x,y,z）是虚拟3D立体坐标上的点，由（x，y，z）到（xP，yP）的过程 就叫 透视投影

K1和K2是根据几何因子得到的常数，这些几何因子包括你的投影平面（clipspace （剪切空间））的宽高比以及你的眼睛的“视野”，并且它们考虑了广角视野的范围。

你能够看到该转换如何对透视进行模拟。 靠近屏幕两侧的点随着与眼睛之间距离（zW）的增加而逐渐被推向中央位置。 与此同时，靠近中央（0，0）的点受到与眼睛之间距离的影响较小并且仍保持靠近中央的位置。（怎么理解呢？举个例子，（x，y，z）中（x，y）不变 Z变化，用生活上的例子描述，在美国大片那种笔直的公路上，公路宽10米，你开车行驶在路中央，观察后面的两边的两个路灯A，B，开始是觉得他们距离好远的 10米啊，随着你越来越远 是不是会感觉到两个路越靠越近？如果有几公里的话 这两个路灯看起来就像是重合一样？）

这种由z轴进行的分割就是众所周知的“透视分割（perspective divide）”。

之前的教程都是假设Z轴等于0，接下来讨论Z轴不等于0的情况：

接着上图，如果使用透视投影的话，则3D虚拟点会投射在CLIPSPACE（剪切空间）如图的位置上：

在2D屏幕上显示的点的位置：

(xP2,yP2) = (K1*x2/z2,K2*y2/z2)；

(xP1,yP1) = (K1*x1/z1,K2*y1/z1);

其实就是简单的矩阵运算(大家没把大学学的线性代数忘记吧？？那么快就丢回给老师了？)，看到这里也许有人迷糊了，什么是3D世界点 什么是2D屏幕点呢？说白一点，3D世界的点 就是你眼睛看到认为它所在的点，2D屏幕上的点 就是其实它真实所在的地方，也就是说 你眼睛在这个时候欺骗了你。其实你的电脑屏幕上永远也没有真实的3D  只是你眼睛一直在欺骗你的神经中枢而已。其中欺骗眼睛赚大钱的技术 就是名声在外的 3D电影技术！

使用矩阵 Using Matrices

在我们编写我们的第一个着色器的时候，我们仅仅把每一个坐标输出到顶点位置（OutPut Position），输出的过程其实就是透视投影 把一个世界坐标的点 输出到剪切空间（Clip Space）上，

我们能够针对一个对象进行 平移（translation）、旋转（rotation）、缩放（scaling）（作者漏了 歪斜（skewing）），但是我们并不能修改它的顶点，这是为什么呢？

A>当Y轴旋转45°的时候，计算顶点的位置会变得非常复杂，因为缩放也随着变成原来的2.37倍

B>在Stage3D中失去任何作用的顶点坐标需要再次上传到顶点缓冲中，渲染三角形之所以那么快，那全是因为在显存（V-RAM 视频存储器？）中做好了全部工作。

相对于于上传新的坐标点到V-RAM，还有一种方式是使用矩阵计算顶点输出位置，矩阵将在每一帧中作为常量上传到V-RAM上，而相对于 上传 纹理（texture），顶点缓冲（Vertex Buffer），常量是上传速度最快的。

改进上一篇的三角形例子：

现在打开上一篇教程中的三角形例子（或者重新下载），让我们使用这一篇学到的新内容去改进它：

第一步是建立Matrix3D对象

并且作为Vertex Constant（顶点常量）上传到显卡（Graphic Card），然后在代码中找到渲染函数rander，在194行的地方，new一个Matrix3D，然后设定是沿着x或者y平移，最后使用context.setProgramConstantsFromMatrix 函数 上传到GPU：

[code lang=”as3″]
m = new Matrix3D();
m.appendTranslation(Math.sin(getTimer()/500)*.5, 0, 0);
context.setProgramConstantsFromMatrix(Context3DProgramType.VERTEX, 0, m, true);[/code]

在appendTranslation的第一个参数中设置根据时间取值，也就是说X轴的数据随着时间变化 编译的时候会看到三角形沿着X轴移动。如果仅仅加入这几句就编译的话  显示的是和上一篇的效果没有任何改变的；

第二步我们需要告诉GPU如何使用Matrix3D矩阵：在顶点着色器中使用

改进顶点着色器（Vertex Shader）

显然改进顶点着色器需要使用到AGAL，现在该学学如何在着色器中使用AGAL编码调用常量了。下面介绍下将要用到的两个新寄存器：

vc : Vextex Constant. 顶点常量寄存器，矩阵Matrix数据大小占4个寄存器，也就是说  如果你设置了vc0，那就必须设置vc1 vc2 vc3。

fc : Fragment Constant.片段常量寄存器，和顶点常量寄存器类似，不过它是针对片段着色器的。

在上一篇的代码例子中 找到顶点着色器的代码部分，在161行，我们使用Matrix3D计算每一个顶点然后输出到常量寄存器中，而并不仅仅是直接把坐标输出到剪切空间。

使用一个4*4的矩阵操作一个顶点，需要用到操作码 m44，m=matrix3D  44=4*4，

[cc lang=”java”]m44 destination, vertex, matrix//操作码 目标点 顶点 矩阵[/cc]

目标点是顶点输出位置（Vertex output Position） 顶点在顶点属性寄存器（va0）中，矩阵在顶点常量寄存器（vc0）中

如下编写AGAL：

[code lang=”as3″]
// VERTEX SHADER
var code:String = “”;
code += “m44 op, va0, vc0\n”; / Perform a 4×4 matrix operation on each vertices
code += “mov v0, va1\n”;[/code]

现在，编译代码 我们将看到三角形沿着X轴来回移动！在之前Matrix3D中我们的x取值是设置在[-0.5,0.5]之间，所以你会看到三角形来回移动

使用一个新类：

在上一部已经解释了通过矩阵变换显示三角形，如果能理解其中的数学原理当然更好，但是不理解也并不太碍事。下面就稍微说下其中的数学原理吧！

如果你没兴趣的话 可以跳过这段，如果你有兴趣的话  那就先跟我一起去下载adobe提供的一个类吧 PerspectiveMatrix3D.

这个类可以在建立Matrix3D矩阵的时候设置参数，首先下载源码 ：HelloMatrix3D，然后看类AddingPerspective.as

AddingPerspective.as其实在屏幕上画一个正方形，这样使得角度对于他的影响更为直观。在上一篇中  你已经知道了如何画三角形  画正方形其实就是画两个三角形，你可以直接看源码而了解到具体的编码步骤，在下一篇文章中在讲诉处理索引的时候我们讲回到正方形，下面的例子无论使用三角形还是正方形都没有任何问题。

The PerspectiveMatrix3D class:

在大部分的情况下，PerspectiveMatrix3D类允许定义四个方面的参数用来呈现不同的属性的情况：

1>FoV：根据fov（field of view，视野区域）角度（定义眼睛广角视野范围的角度），fov代表的视野的宽度，我们这里定义为45°

2>宽高比，即是：width/height

3>zNear  Z轴的最小有效坐标（眼睛能看清舞台的最近距离），在这里设置为0.1  稍后还要详细解释它

4>zFar   Z轴最大的有效坐标，（眼睛最远能看到的距离），在这里设置为1000

在源码的render函数里设置如下：

[code lang=”as3″]

var projection:PerspectiveMatrix3D = new PerspectiveMatrix3D();
projection.perspectiveFieldOfViewLH(45*Math.PI/180, 4/3, 0.1, 1000);
[/code]

About the zNear:

上面已经解释了为什么Z不能从0开始，下面先记住透视投影公式：

[cc lang=”java”]
xP = K1 * x / z
yP = K2 * y / z
[/cc]

既然Z做除数那肯定不能为零，上一节的教程中 是由于2D 对象的 z 属性的值为零，并且其 matrix3D 属性的值为 null。但是3D中Z只能取一个最小值，下面看一段代码：

[code lang=”as3″]
var projection:PerspectiveMatrix3D = new PerspectiveMatrix3D();
projection.perspectiveFieldOfViewLH(45*Math.PI/180, 4/3, 0.1, 1000);

m = new Matrix3D();
m.appendRotation(getTimer()/30, Vector3D.Y_AXIS);
m.appendRotation(getTimer()/10, Vector3D.X_AXIS);
m.appendTranslation(0, 0, 2);
m.append(projection);[/code]

编译，可以理解为显示的是一个旋转的三角形，但是其实显示的是一个旋转的正方体

像往常一样,一个小练习是最好的学习方式：

1>在有效区间设置R,G,B的值  （[0，1]），上传一个[225，225，225，225]的片段着色常量，在输出到片段oc寄存器之前先除以颜色值（使用div指令）

（这个题目我不太懂  等多了解下AGAL再回来做）

这篇教程我写的代码很少，原因是我相信：

A，我写的越少 你写的越多

B，每次都解释每一行代码太费劲（意思读者应该学会举一反三 自己理解）

往下的教程中，都会把这篇的代码类作为基础增删改。

总结：

这篇文章作者主要是分析Z轴的作用  还有就是加入矩阵变换，是一比较抽象的技术点，理解的时候要多看代码 多改 多编译看效果~